Introduction
Knowing how to find domain of a function is an essential skill in mathematics. It helps you avoid errors and understand where the function is defined.
Why is it important to know how to find the domain of a function? By identifying the correct domain, you ensure that you’re using the function correctly, especially with more complex functions involving square roots or fractions.
In this guide, we’ll show you how to find the domain of a function step by step. With clear explanations and easy-to-follow examples, you’ll master how to find the domain of a function quickly and confidently.
Let’s get started! 🚀
What is the Domain of a Function?
Before we dive into the steps of how to find domain of a function, let’s understand the basic idea.
The domain refers to all the possible values of x (inputs) that a function can accept. Simply put, it’s the set of numbers you can plug into the function without causing any errors. Knowing how to find domain of a function helps avoid mistakes, especially with more complex functions involving square roots or fractions.
For example, in a linear function like
x can be any real number. So, the domain is all real numbers. Easy, right? 😄
However, some functions have restrictions:
In a rational function like
x cannot be 3 because division by zero is undefined.
For square root functions, such as
the value inside the square root must be non-negative, so x must be 2 or greater.
Understanding these rules is key to learning how to find domain of a function. For a deeper dive into different types of functions, check out Khan Academy’s guide on domain.
In the next section, we’ll break down the exact steps to find the domain of any function. Let’s go! 🚀.
Different Functions and Steps to Find Their Domain
Knowing how to find domain of a function involves understanding different types of functions and applying specific steps to identify any restrictions.
Let’s break this down by function type, with clear steps and examples.
Linear Functions: How to Find Domain of a Function
Linear functions are one of the simplest types of functions. They have the form:
Where m is the slope and b is the y-intercept. The key thing to remember is that linear functions don’t have any restrictions on their domain. You can plug in any real number for x without causing any problems.
Steps to Find the Domain of a Linear Function
- Step 1: Identify the type of function: In this case, it’s a linear function.
- Step 2: Check for restrictions: For linear functions, there are no restrictions. There’s nothing that could cause division by zero, square roots of negative numbers, or other issues.
- Step 3: Write the domain: Since there are no restrictions, the domain of a linear function is all real numbers.
In interval notation, this would be written as:
This simply means that any value of x can be used in the function.
Example: How to Find Domain of a Linear Function
Let’s take an example:
Step 1: Identify the Type of Function
This function is linear because it follows the form f(x)=mx+b, where m=3 and b=−7.
Step 2: Check for Restrictions
Linear functions have no restrictions. Unlike rational or square root functions, there are no fractions or square roots to worry about. So, there’s no value of x that would make the function undefined.
Step 3: Write the Domain
Since there are no restrictions, the domain includes all real numbers. We express this as:
This means you can plug in any number for x—positive, negative, fractions, or decimals—and the function will work just fine!
Linear functions are the simplest when learning how to find domain of a function. They set a good foundation for understanding more complex functions, where you’ll need to consider restrictions.
Want more practice with linear functions? Check out this Libretext resource on domains.
You Should Also Read: Math Classes in High School Order: Algebra to Calculus
Rational Functions: How to Find Domain of a Function
Rational functions are a bit more complex than linear functions. They have the form:
Where P(x) and Q(x) are polynomials. The key thing to remember is that the denominator Q(x) cannot be zero. This is important because division by zero is undefined. Understanding this is crucial when learning how to find domain of a function.
Steps to Find the Domain of a Rational Function
Step 1: Identify the type of function
In this case, it’s a rational function because it involves a fraction with polynomials in the numerator and denominator.
Step 2: Check for restrictions
The main restriction in a rational function is that the denominator cannot be zero. So, we need to set the denominator equal to zero and solve for x to find any values that must be excluded.
Step 3: Write the domain
After finding the restricted values, the domain includes all real numbers except those values. We express this using interval notation.
Example: How to Find Domain of a Rational Function
Let’s take an example:
Step 1: Identify the type of function
This is a rational function because it involves a fraction.
Step 2: Check for restrictions
We need to make sure the denominator is not zero. Set the denominator equal to zero and solve for x:
This means x cannot be 3 because it would make the denominator zero, which is undefined.
Step 3: Write the domain
Since x cannot be 3, the domain includes all real numbers except 3. In interval notation, we write:
This means you can plug in any number for x except 3—positive, negative, fractions, or decimals—and the function will work fine.
Why This Matters
Learning how to find domain of a function, especially rational ones, is important for avoiding undefined values. Understanding this concept will help you build a strong foundation for more complex math topics.
For more practice and detailed examples on rational functions, you can check out Byjus guide on rational function domains.
Do one more problem to find out the domain of the rational functions by watching this video –
Square Root Functions: How to Find Domain of a Function
Square root functions introduce a new challenge when learning how to find domain of a function. These functions have the form:
The key thing to remember is that the expression inside the square root must be non-negative. In other words, it has to be greater than or equal to zero. This is because you can’t take the square root of a negative number and get a real result.
Steps to Find the Domain of a Square Root Function
Step 1: Identify the type of function
In this case, it’s a square root function.
Step 2: Check for restrictions
Set the expression inside the square root greater than or equal to zero. Solve this inequality to find the values of x that work.
Step 3: Write the domain
The domain will include the values of x that satisfy the inequality. Express the solution in interval notation.
Example: How to Find Domain of a Square Root Function
Let’s take an example:
Step 1: Identify the type of function
This is a square root function because it has a square root symbol.
Step 2: Check for restrictions
The expression inside the square root is x−2x – 2. To ensure it’s non-negative, set it greater than or equal to zero:
This means x must be 2 or greater.
Step 3: Write the domain
The domain includes all values of x that are greater than or equal to 2. In interval notation, we write:
This means you can plug in any number for x as long as it’s 2 or more, and the function will work fine.
Why This Matters
Understanding how to find domain of a function for square root functions is important because it helps avoid undefined values. Square root functions teach you to consider inequalities, which are essential for more advanced math concepts.
Watch this video to understand it better –
Logarithmic Functions: How to Find Domain of a Function
Logarithmic functions introduce another important concept when learning how to find domain of a function. These functions have the form:
The key thing to remember is that the expression inside the logarithm must be positive. Logarithms are only defined for positive numbers, so any value that makes the argument zero or negative is not part of the domain.
Steps to Find the Domain of a Logarithmic Function
Step 1: Identify the type of function
In this case, it’s a logarithmic function because it involves a log expression.
Step 2: Check for restrictions
Set the expression inside the logarithm greater than zero. Solve this inequality to find the values of x that work.
Step 3: Write the domain
The domain will include the values of x that satisfy the inequality. Express the solution in interval notation.
Example: How to Find Domain of a Logarithmic Function
Let’s take an example:
Step 1: Identify the type of function
This is a logarithmic function because it has a log expression.
Step 2: Check for restrictions
The expression inside the logarithm is x−5x – 5. To ensure it’s positive, set it greater than zero:
This means x must be greater than 5.
Step 3: Write the domain
The domain includes all values of x that are greater than 5. In interval notation, we write:
This means you can plug in any number for x as long as it’s greater than 5, and the function will work fine.
Why This Matters
Understanding how to find domain of a function for logarithmic functions is crucial because it reinforces the concept of positivity. Logarithmic functions help you practice inequalities, which are essential for solving more complex problems in calculus and beyond.
You Should Also Read: SAT Math Formula Sheet: Formulas for Test Success in 2024
Exponential Functions: How to Find Domain of a Function
Exponential functions are straightforward when it comes to understanding how to find domain of a function. These functions have the form:
where a is a positive constant, and xx can be any real number. The key thing to remember is that exponential functions are defined for all real values of x. There are no restrictions or undefined values to consider.
Steps to Find the Domain of an Exponential Function
Step 1: Identify the type of function
In this case, it’s an exponential function because the variable x is in the exponent.
Step 2: Check for restrictions
Exponential functions do not have any restrictions on their domain. There are no values of x that will make the function undefined.
Step 3: Write the domain
Since there are no restrictions, the domain of an exponential function includes all real numbers. In interval notation, this is expressed as:
Example: How to Find Domain of an Exponential Function
Let’s take an example:
Step 1: Identify the type of function
This is an exponential function because xx is the exponent.
Step 2: Check for restrictions
There are no restrictions for exponential functions. The base (2 in this case) is positive, and the exponent can be any real number.
Step 3: Write the domain
Since there are no restrictions, the domain includes all real numbers:
This means you can plug in any value for x—positive, negative, fractions, or decimals—and the function will work without any issues.
Why This Matters
Understanding how to find domain of a function for exponential functions is essential because it shows that not all functions have restrictions. This concept is a fundamental building block for more advanced topics in math and science, such as growth models and decay processes.
Domain of a Function from its Graph
Finding the domain of a function from its graph involves identifying all the possible input values for which the function is defined and has a valid output. This is achieved by examining the x-values over the entire graph. Here’s a step-by-step guide on how to find the domain of a function from its graph:
Step 1: Identify the X-axis Range
Look at the x-axis of the graph to determine the range of x-values that are visible in the graph. The domain will generally be a subset of this range, but there may be exceptions where we exclude certain x-values.
Step 2: Note Any Vertical Asymptotes or Holes
Vertical asymptotes and holes in the graph can indicate excluded x-values from the domain. Vertical asymptotes are vertical lines where the function approaches infinity or negative infinity, indicating that the function is undefined at those points. Holes are points on the graph where there is an open circle, indicating that the function’s value does not exist at that specific x-value.
Step 3: Account for Any Discontinuities
Discontinuities in the graph can also signify excluded x-values from the domain. Discontinuities occur where the function has breaks or jumps and may be due to removable or non-removable singularities.
Step 4: Combine the Information
Based on the steps above, identify all the x-values that we need to exclude from the range determined in Step 1. The domain of the function will be all the x-values that remain after accounting for vertical asymptotes, holes, and discontinuities.
Example:
Let’s work through an example to find the domain of a function from its graph:
Consider the graph of the function f(x) shown below:
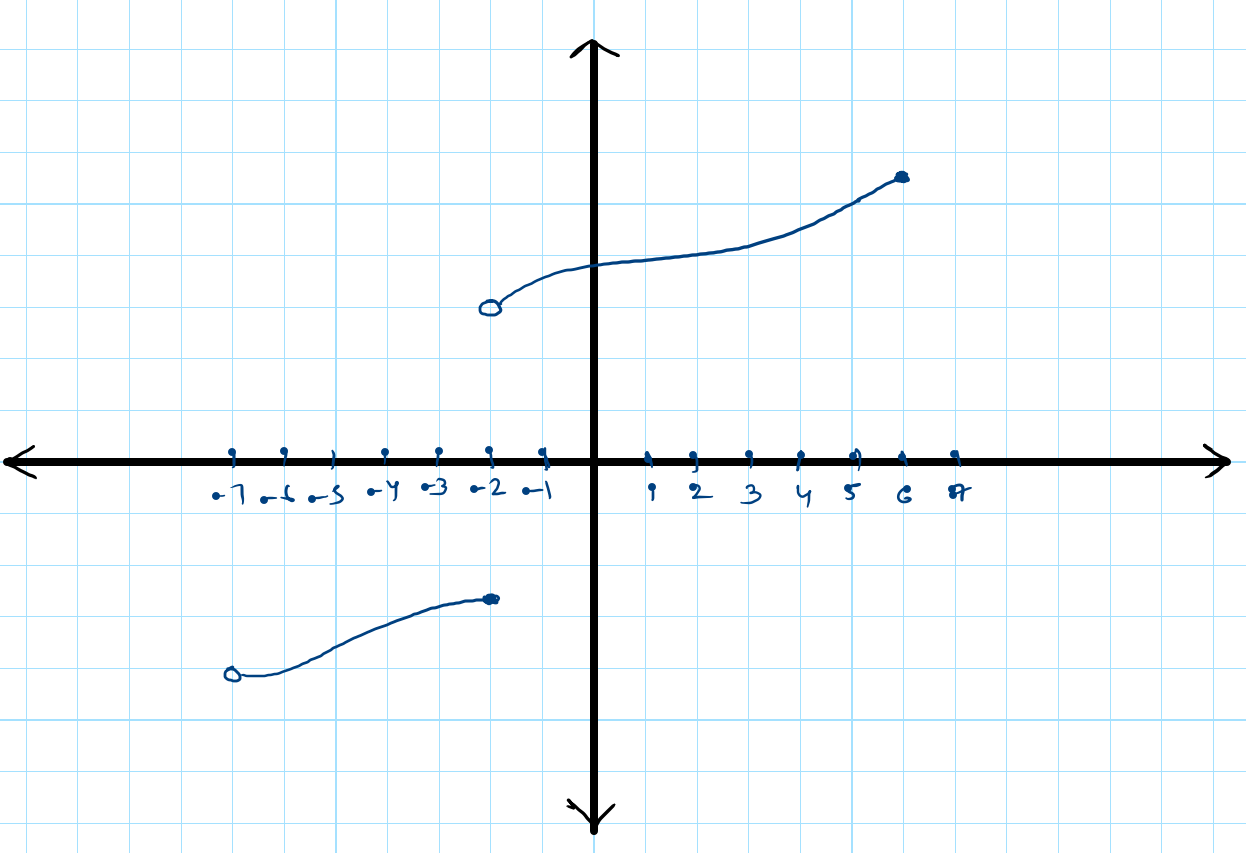
Step 1: Identify the X-axis range from the graph, we can see that the X-axis covers a range from -7 to 6.
Step 2: Note any Vertical Asymptotes or Holes. There are 2 holes in the graph, at x = -7 and x = -2 where there is an open circle. But at x = -2, the function is having a closed circle as well. So x can be -2.
Step 3: Account for any Discontinuities. The graph does not show any obvious discontinuities.
Step 4: Combine the information gathered, the excluded x-values from the domain are x = -7.
Therefore, the domain of the function f(x) from its graph is (-7, to 6].
Watch this video for ste-by-step explanation of the above problem –
Common Mistakes to Avoid When Finding the Domain of a Function
When learning how to find domain of a function, students often make some common mistakes. Understanding these will help you avoid errors and build a solid foundation:
- Ignoring Denominator Rules in Rational Functions:
Always check that the denominator is not zero. Forgetting this can lead to undefined values. - Overlooking Negative Values in Square Root Functions:
Ensure the expression inside the square root is non-negative. Students often forget to set the inequality correctly. - Misinterpreting Logarithmic Restrictions:
Remember that the argument of a logarithm must be positive, not just non-negative. Zero and negative numbers are not allowed inside the log. - Forgetting to Consider All Parts of Piecewise Functions:
For piecewise functions, examine each piece separately and combine their domains carefully. Missing one piece can lead to an incomplete domain. - Incorrect Interval Notation:
Be careful with your notation. For example, use brackets [ ] for inclusive values (like square roots) and parentheses ( ) for values that aren’t included (like open intervals in rational functions). - Assuming Restrictions in Exponential Functions:
Exponential functions have no restrictions, but students sometimes look for nonexistent issues.
Conclusion
Learning how to find domain of a function is a fundamental skill in mathematics. Understanding domains helps ensure you avoid undefined values and solve problems accurately. From linear and rational functions to square roots and logarithms, each type has unique rules you need to remember. By practicing these steps and avoiding common mistakes, you’ll build a strong foundation for more advanced math topics.
Ready to dive deeper? Explore more examples and exercises on sites like Khan Academy and Math is Fun. Keep practicing, and soon, finding the domain of any function will be second nature! 🚀



